Queue (Hàng đợi)

Hàng đợi (tiếng Anh: Queue) là cấu trúc dữ liệu đúng như cái tên nó mô tả, giống như hành động xếp hàng của chúng ta, nhưng không có chuyện ai đó chen vào giữa hàng hay chờ lâu quá bỏ hàng đi về.

Hình ảnh hàng đợi trong thực tế

Hàng đợi hoạt động theo nguyên tắc (FIFO) - First-In-First-Out, đến trước được phục vụ trước; Khác với Ngăn xếp theo nguyên tắc LIFO mà chúng ta đã tìm hiểu trước đó.

Hàng đợi (queue) là gì?

Như đã trình bày ở trên, hàng đợi là cấu trúc dữ liệu chỉ cho phép can thiệp ở 2 đầu, một đầu là thêm dữ liệu mới, thì đầu còn lại là lấy dữ liệu ra - đồng nghĩa là dữ liệu đã ở trong hàng đợi lâu nhất.

Như vậy, với cấu trúc dữ liệu hàng đợi, chúng có 2 phương thức để chúng ta thao tác:

Thêm dữ liệu vào 1 đầu, tùy vào ngôn ngữ lập trình mà nó có tên gọi khác nhau, có thể là push, add, enqueue, ... nhưng chỉ là khác tên phương thức.
Lấy dữ liệu ra ở đầu còn lại, phương thức này cũng có nhiều cái tên như pop, remove, dequeue, ...

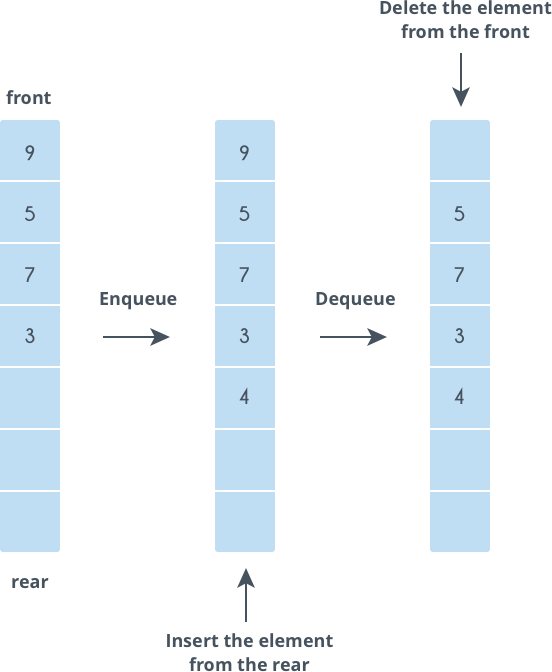
Mô phỏng hoạt động hàng đợi

Quan sát ảnh phía trên, khi bạn:

Thêm phần tử vào cuối hàng đợi, chỉ số có rear sẽ tăng lên.
Khi bạn xóa phần tử khỏi hàng đợi, chỉ số front cũng sẽ tăng lên.
Vì hàng đợi là dãy số liên tiếp từ front đến rear, nên để lấy size thì bạn sẽ tính khoảng cách giữa rear và front.

📚 Lưu ý: Hàng đợi có 2 đầu và việc chọn đầu nào để thêm dữ liệu cũng được, khi đó đầu còn lại sẽ đảm nhiệm vai trò còn lại.

Tương tự Ngăn xếp, chúng ta cũng có các hàm hỗ trợ như

IsFull() để kiểm tra hàng đợi đã đầy
IsEmpty() để kiểm tra hàng đợi chưa có dữ liệu
Size() để lấy kích thước hiện tại của hàng đợi

⚠️ Lý thuyết trên đây là hàng đợi phiên bản gốc, chúng ta cũng có biến thể hàng đợi 2 đầu, khi đó chức năng thêm và lấy dữ liệu đều có trên cả 2 đầu, sẽ tìm hiểu ở mục tiếp theo.

Cài đặt hàng đợi

Ở mục này, chúng ta sẽ thực hiện cài đặt các chức năng của Queue đã nói ở phần trước. Mục này tôi sẽ cùng các bạn đi cài đặt queue bằng mảng trong C/C++, bởi vì nó sẽ đơn giản hơn, giúp các bạn dễ hiểu hơn. Các cách cài đặt khác sẽ được trình bày ở phần sau.

Để cài đặt được Queue, chúng ta sẽ cần sử dụng các biến như sau:

queue[]: Một mảng một chiều lưu dữ liệu của hàng đợi, sẽ khai báo trong hàm main sau.
MAX_SIZE: Số lượng phần tử tối đa có thể lưu trữ trong hàng đợi
front: Chỉ số của phần tử ở đang đầu queue. Nó sẽ là chỉ số của phần tử sẽ bị xóa ở lần tiếp theo
rear: Chỉ số của phần tử tiếp theo sẽ được thêm vào cuối của queue

const int MAX_SIZE = 7;
int front = 0; // chỉ số đầu
int rear = 0; // chỉ số cuối

Bây giờ ta sẽ đi vào cài đặt từng chức năng của Hàng đợi.

Các hàm phụ trợ

bool isEmpty() {
    return front == rear;
}

bool isFull() {
    return rear == MAX_SIZE;
}

int Size() {
    // mình đang cài đặt rear là chỉ số mảng của phần tử tiếp theo, nên không cần cộng thêm 1 ở đây.
	// Ví dụ front đang là 0, mảng có 3 phần tử (0, 1, 2) thì rear cuả mình đang là 3.
    return rear - front; 
}

Thêm vào cuối hàng đợi

Nếu hàng đợi chưa đầy, chúng ta sẽ thêm phần tử cần thêm vào cuối(rear) của hàng đợi. Ngược lại, thông báo lỗi.

void push(int queue[], int value) {
    if (isFull()) {
        printf("Queue is full\n");
        return;
    }
    // queue[rear++] = value; // tương tự 2 lệnh dưới
    queue[rear] = value;
    rear++;
}

Lấy dữ liệu ra khỏi hàng đợi

Nếu hàng đợi có ít nhất 1 phần tử, chúng ta sẽ tiến hành lấy và xóa bỏ phần tử ở đầu của hàng đợi bằng cách tăng front lên 1 giá trị.

int pop(int queue[]) {
    if (isEmpty()) {
        printf("Queue is empty\n");
        return NULL;
    }
    int value = queue[front];
    front++; // Chỗ này là cộng chứ không phải trừ
    return value;
}

Mã nguồn kèm hàm main

// Hàng đợi - C++
#include <stdio.h>

const int MAX_SIZE = 7;
int front = 0; // chỉ số đầu
int rear = 0; // chỉ số cuối

bool isEmpty() {
    return front == rear;
}

bool isFull() {
    return rear == MAX_SIZE;
}

int size() {
    return rear - front;
}

void push(int queue[], int value) {
    if (isFull()) {
        printf("Queue is full\n");
        return;
    }
    // queue[rear++] = value;
    queue[rear] = value;
    rear++;
}

int pop(int queue[]) {
    if (isEmpty()) {
        printf("Queue is empty\n");
        return NULL;
    }
    int value = queue[front];
    front++; // Chỗ này là cộng chứ không phải trừ
    return value;
}

int main(){
    int queue[MAX_SIZE];
    push(queue, 9);
    push(queue, 5);
    push(queue, 7);
    push(queue, 3);
    printf("Size: %d\n", size());
    push(queue, 4);
    printf("Size: %d\n", size());
    int value = pop(queue);
    printf("Pop: %d\n", value);
    printf("Size: %d\n", size());
    return 0;
}

Chạy chương trình:

Size: 4
Size: 5
Pop: 9
Size: 4

Thực hành với hàng đợi

Để hiểu rõ hơn cấu trúc dữ liệu queue, chúng ta sẽ đi vào một bài toán cụ thể như sau:

Bạn có một chuỗi ký tự. Hãy lấy ký tự ở đầu của chuỗi và thêm nó vào cuối chuỗi. Hãy cho tôi thấy sự thay đỗi của chuỗi sau khi thực hiện hành động trên N lần.

Ý tưởng: Chuỗi ký tự trên có thể xem xét như là một hàng đợi. Tại mỗi bước, chúng ta sẽ pop(xóa) phần tử ở đầu chuỗi và thực hiện push(thêm) phần tử đó cuối chuỗi. Lặp lại N lần bước công việc này, chúng ta sẽ có câu trả lời.

Lời giải:

 // Ngăn xếp (Stack) - CPP
#include <stdio.h>

const int MAX_SIZE = 7;
int front = 0; // chỉ số đầu
int rear = 0; // chỉ số cuối

bool isEmpty() {
    return front == rear;
}

bool isFull() {
    return rear == MAX_SIZE;
}

int size() {
    return rear - front;
}

void push(char queue[], char value) {
    if (isFull()) {
        printf("Queue is full\n");
        return;
    }
    // queue[rear++] = value;
    queue[rear] = value;
    rear++;
}

char pop(char queue[]) {
    if (isEmpty()) {
        printf("Queue is empty\n");
        return NULL;
    }
    char value = queue[front];
    front++; // Chỗ này là cộng chứ không phải trừ
    return value;
}

int main(){
    char queue[MAX_SIZE];
    push(queue, 'a');
    push(queue, 'b');
    push(queue, 'c');
    push(queue, 'd');
    printf("Size: %d\n", size());
    int N = 3; // thực hiện 3 lần
    for (int i = 0; i < N; i++) {
        char c  = pop(queue);
        printf("pop: %c\n", c);
        push(queue, c);
    }
    // print all
    while (!isEmpty()) {
        printf("%c ", pop(queue));
    }
    return 0;
}

Kết quả:

Size: 4
pop: a
pop: b
pop: c
d a b c

Ứng dụng của hàng đợi

Hàng đợi được sử dụng rất nhiều và nó giống như cách mà chúng ta xếp hàng ở nơi tốc độ xử lý chậm hơn nhu cầu thực tế. Thực tế này cũng xảy ra trong lập trình (hoặc chí ít là chúng ta áp dụng để đề phòng cho trường hợp đó).

Máy in sử dụng hàng đợi để quản lý các nhiệm vụ in, lệnh nào tới trước sẽ được xử lý trước.
Hệ điều hành cũng dùng hàng đợi để xử lý các công việc của nó.
Thuật toán tìm kiếm theo chiều rộng - BFS cũng dùng hàng đợi để cài đặt.
Và rất nhiều công cụ / thư viện áp dụng cơ chế hàng đợi như: Load Balancer (Cân bằng tải), Kafka / RabbitMQ, Redis, ... để phục vụ cho phát triển phần mềm.

ứng dụng của hàng đợi

Circular queue(Hàng đợi vòng)

Đây là cách cài đặt nâng cao giúp hàng đợi tận dụng tối đa bộ nhớ.

Quan sát cài đặt phía trên, khi lấy (pop) dữ liệu khỏi hàng đợi, chúng ta tăng chỉ số front lên, thêm thì chúng ta tăng chỉ số rear lên, như vậy vùng nhớ từ chỉ số 0 đến front sẽ bị lãng phí.

Cách cài đặt này sẽ khắc phục điểm yếu đó.

Hàng đợi vòng là một cải tiến của hàng đợi tiêu chuẩn. Trong hàng đợi tiêu chuẩn, khi một phần tử bị xóa khỏi hàng đợi, các vị trí bị xóa đó sẽ không được tái sử dụng. Hàng đợi vòng sinh ra để khắc phục sự lãng phí này.

Hàng đợi vòng sử dụng lại các vị trí đã bị xóa ở đầu mảng file

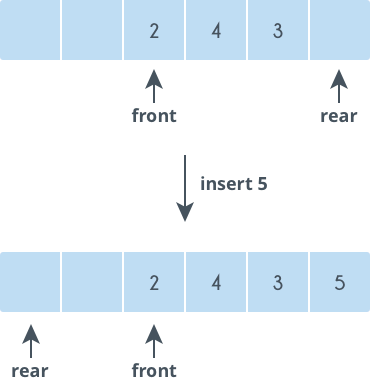
Trong khi thêm phần tử vào hàng đợi vòng, nếu chỉ số rear đã ở vị trí cuối của mảng, khi đó bạn vẫn có thể thêm vào hàng đợi bằng cách thêm vào phía đầu của mảng (đó là các vị trí ở đầu mảng đã bị xóa đi và chưa được dùng).

Để cài đặt hàng đợi vòng, ngoài các biến sử dụng trong hàng đợi tiêu chuẩn, chúng ta cần thêm một biến khác nữa để lưu số lượng phần tử đang có trong hàng đợi, đặt nó là count

Bây giờ chúng ta cùng đi viết các hàm cho hàng đợi vòng nhé.

void push(char queue[], int value) {
    if (isFull()) {
        printf("Queue is full\n");
        return;
    }
    queue[rear] = value;
    rear = (rear + 1) % MAX_SIZE;
    count++;
}

Mình giải thích tại sao lại là (rear + 1) % MAX_SIZE: Giả sử khi rear = arraySize - 1, khi đó với hàng đợi tiêu chuẩn bạn sẽ không thể thêm nữa. Nhưng với hàng đợi vòng, ta sẽ thêm chừng nào count < MAX_SIZE. MAX_SIZE là số phần tử tối đa có thể có, do vậy, count < MAX_SIZE nghĩa là còn ô trống để insert vào queue.

Chỉ số được insert vào queue như sau(giả sử MAX_SIZE = 3 nhé):

Nếu rear = 0, giá trị rear thực là (0 + 1) % 3 = 1
Nếu rear = 1, giá trị rear thực là (1 + 1) % 3 = 2
Nếu rear = 2, giá trị rear thực là (2 + 1) % 3 = 0

⚠️ Các bạn cần nhớ: rear là chỉ số của phần tử sẽ được insert ở lần tiếp theo. Mỗi khi pop, count sẽ phải giảm đi 1. Ngược lại, nếu push thành công, count sẽ tăng lên 1.

Giải thích này cũng đúng với front trong hàm pop dưới đây.

int pop(char queue[]) {
    if (isEmpty()) {
        printf("Queue is empty\n");
        return NULL;
    }
    int value = queue[front];
    front = (front + 1) % MAX_SIZE;
    count--;
    return value;
}

Dưới đây là cài đặt đầy đủ đi kèm hàm main

#include <stdio.h>

const int MAX_SIZE = 4;
int front = 0; // chỉ số đầu
int rear = 0; // chỉ số cuối
int count = 0;

bool isEmpty() {
    return count == 0;
}

bool isFull() {
    return count == MAX_SIZE;
}

int size() {
    return count;
}

void push(char queue[], int value) {
    if (isFull()) {
        printf("Queue is full\n");
        return;
    }
    queue[rear] = value;
    rear = (rear + 1) % MAX_SIZE;
    count++;
}

int pop(char queue[]) {
    if (isEmpty()) {
        printf("Queue is empty\n");
        return NULL;
    }
    int value = queue[front];
    front = (front + 1) % MAX_SIZE;
    count--;
    return value;
}

int main(){
    char queue[MAX_SIZE];
    push(queue, 1);
    push(queue, 2);
    push(queue, 3);
    push(queue, 4);
    push(queue, 5); // full here
    printf("Size: %d\n", size());
    printf("Pop: %d\n", pop(queue));
    push(queue, 5); // now not full
    printf("Size: %d\n", size());
    return 0;
}

Kết quả thực thi

Queue is full
Size: 4
Pop: 1
Size: 4

Hàng đợi 2 đầu

Trong hàng đợi tiêu chuẩn phía trên, dữ liệu được thêm ở cuối và xóa đi ở đầu của hàng đợi. Nhưng với Double-ended queue, dữ liệu có thể thêm hoặc xóa ở cả đầu(front) và cuối(rear) của hàng đợi.

Nào, hãy cùng tôi đi cài đặt các hàm cho các chức năng của queue 2 đầu nào.

// Hàng đợi 2 đầu

#include <stdio.h>

#define MAX_SIZE 100

int top = 0;
int rear = 0;

int size() {
    return rear - top;
}

int isEmpty() {
    return size() == 0;
}

int isFull() {
    return size() == MAX_SIZE;
}

void push_rear(int queue[], int value) {
    if (isFull()) {
        printf("Queue is full\n");
        return;
    }
    queue[rear++] = value;
}

void push_front(int queue[], int value) {
    if (isFull()) {
        printf("Queue is full\n");
        return;
    }
    for (int i = rear; i > top; i--) {
        queue[i] = queue[i - 1];
    }
    queue[top] = value;
    rear++;
}

int pop_rear(int queue[]) {
    if (isEmpty()) {
        printf("Queue is empty\n");
        return -1;
    }
    return queue[--rear];
}

int pop_front(int queue[]) {
    if (isEmpty()) {
        printf("Queue is empty\n");
        return -1;
    }
    return queue[top++];
}

int get_rear(int queue[]) {
    if (isEmpty()) {
        printf("Queue is empty\n");
        return -1;
    }
    return queue[rear - 1];
}

int get_front(int queue[]) {
    if (isEmpty()) {
        printf("Queue is empty\n");
        return -1;
    }
    return queue[top];
}

int main() {
    int queue[MAX_SIZE];
    push_rear(queue, 1);
    push_rear(queue, 2);
    push_rear(queue, 3);
    push_rear(queue, 4);
    push_rear(queue, 5);
    printf("Front: %d\n", get_front(queue));
    printf("Rear: %d\n", get_rear(queue));
    printf("Pop front: %d\n", pop_front(queue));
    printf("Pop rear: %d\n", pop_rear(queue));
    printf("Front: %d\n", get_front(queue));
    printf("Rear: %d\n", get_rear(queue));
    return 0;
}

Kết quả thực thi:

Front: 1
Rear: 5
Pop front: 1
Pop rear: 5
Front: 2
Rear: 4

Bài tập thực hành

Các bạn hãy thực hành các bài tập về hàng đợi trên LCOJ tại đây nhé. file

Hàng đợi (queue) là gì?​

Cài đặt hàng đợi​

Các hàm phụ trợ​

Thêm vào cuối hàng đợi​

Lấy dữ liệu ra khỏi hàng đợi​

Mã nguồn kèm hàm main​

Thực hành với hàng đợi​

Ứng dụng của hàng đợi​

Circular queue(Hàng đợi vòng)​

Hàng đợi 2 đầu​

Bài tập thực hành​