Breadth-First Search

1. Introduction

What is BFS?

Breadth-First Search (BFS) is one of the fundamental algorithms used for traversing or searching through graphs and trees. It explores nodes layer by layer, moving horizontally across the breadth of the data structure before descending to the next level. The BFS algorithm uses a queue to keep track of the nodes that are yet to be explored, ensuring that it processes nodes at the same level before moving to the next level.

In essence, BFS works like a wave radiating outward from the source node, exploring each neighboring node before moving on to their neighbors.

Where is BFS used?

BFS is widely used in a variety of applications:

• Shortest Path Calculation: BFS is optimal for finding the shortest path in unweighted graphs, as it explores all nodes layer by layer.
• Social Networks: It can be used to discover the degrees of separation between users.
• Web Crawling: BFS can be used to crawl websites, starting from a given web page and exploring its links.
• Maze Solving: BFS can find the shortest path to the exit in mazes and puzzles.

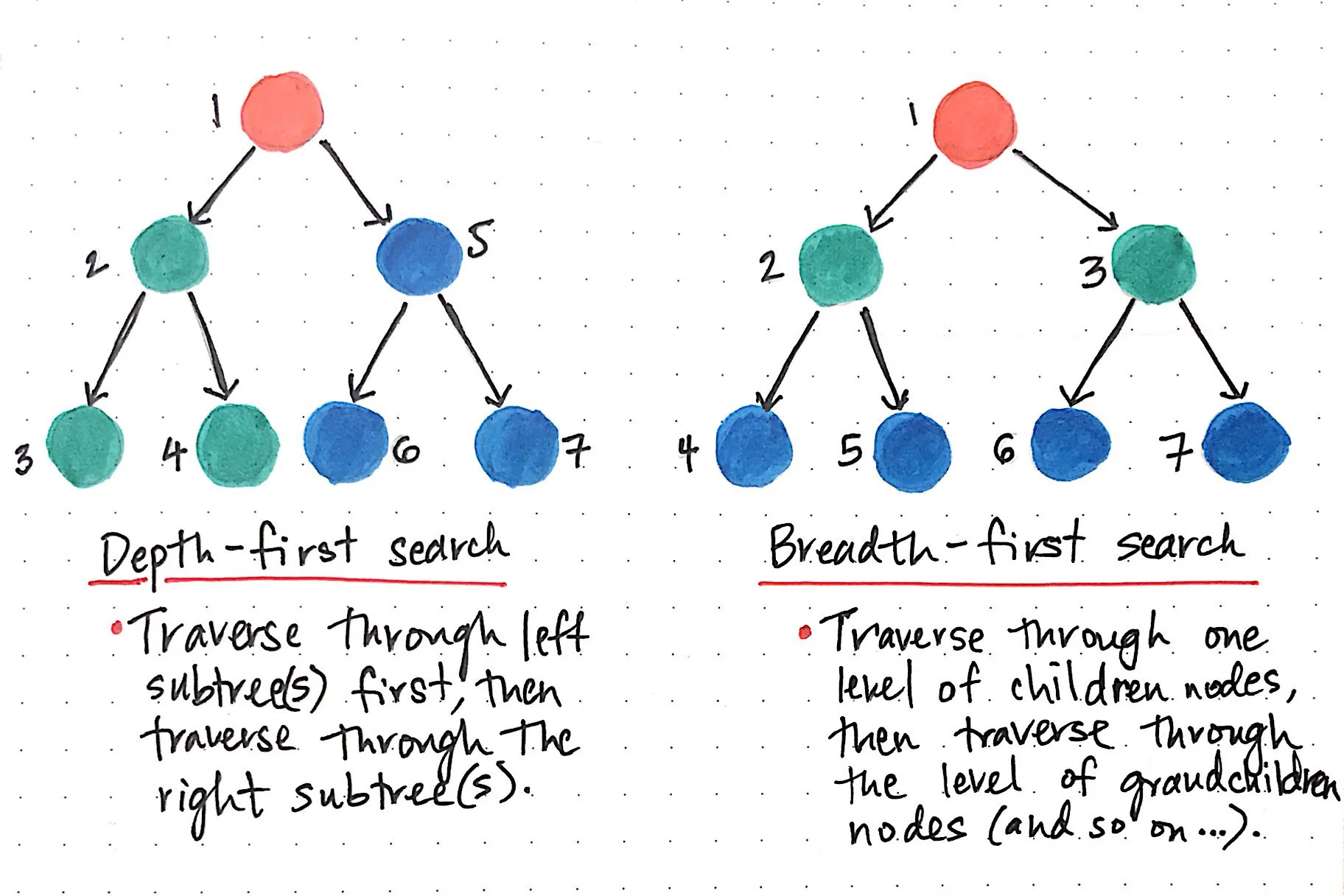
BFS vs. Depth-First Search (DFS)

BFS and DFS are both algorithms for traversing or searching graphs and trees, but they operate differently:

• BFS explores all nodes at the present depth level before moving on to nodes at the next depth level.
• DFS dives deep into one branch of the graph, exploring as far as possible before backtracking and exploring the next branch.

BFS vs. DFS traversal comparison, source: Medium

2. Key Concepts of BFS

Graphs and Trees in BFS

BFS is a versatile algorithm applicable to both graphs and trees:

• A graph is a collection of nodes (or vertices) connected by edges, which may be directed or undirected.
• A tree is a special type of graph without cycles, typically representing hierarchical data structures.

BFS can be applied to both directed and undirected graphs. In the case of trees, BFS is used to explore nodes level by level, making it ideal for finding the shortest path or traversing all nodes in a structured way.

Nodes, Edges, and Levels

In BFS:

• Nodes (or vertices) represent entities (like people, web pages, or puzzle states).
• Edges are the connections between nodes.
• Levels refer to the distance from the source node. BFS explores each level in its entirety before moving on to the next.

Queue Data Structure in BFS

BFS relies heavily on the queue data structure. A queue operates on a First-In, First-Out (FIFO) principle, which aligns perfectly with the layer-by-layer traversal of BFS. The nodes are enqueued as they are discovered and dequeued when they are processed.

[IMAGE description="Illustration of how a queue is used in BFS to manage node exploration, showing enqueuing and dequeuing operations."]

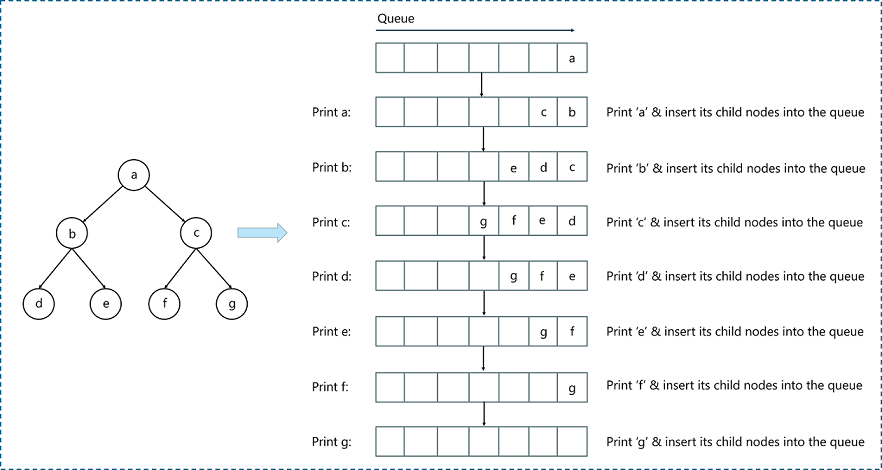
How a queue is used in BFS to manage BFS node exploration, source: Edureka

tip

Read more about Queue Data Structure, note that this post in Vietnamese language.

3. How BFS Works: Step-by-Step Explanation

Exploring Neighboring Nodes

BFS begins at the source node and explores all its neighboring nodes. These nodes are added to the queue for further exploration.

1. Start at the source node.
2. Explore all directly connected nodes (neighbors).
3. Mark them as visited to avoid reprocessing.

Layer-by-Layer Traversal

Once all nodes at the current level are explored, BFS proceeds to the next layer:

1. Dequeue a node from the queue.
2. Explore its unvisited neighbors, adding them to the queue.
3. Repeat until the queue is empty.

Termination Condition

BFS terminates when there are no more nodes left to explore (i.e., when the queue is empty). It also stops early if the target node is found (in cases such as pathfinding).

4. BFS Algorithm

Pseudocode for BFS

Below is the pseudocode for BFS:

BFS(graph, start_node):
    Initialize an empty queue Q
    Initialize an empty set visited
    Enqueue start_node into Q
    Add start_node to visited
    
    while Q is not empty:
        current_node = Dequeue Q
        for each neighbor of current_node:
            if neighbor is not in visited:
                Enqueue neighbor into Q
                Add neighbor to visited

Time and Space Complexity

• Time Complexity: O(V + E), where V is the number of vertices and E is the number of edges. Each vertex and edge is processed once.
• Space Complexity: O(V) for the visited set and the queue, which at worst may hold all the nodes.

5. Implementing BFS in C++

BFS for Trees

Below is an implementation of BFS for a tree structure in C++:

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

struct Node {
    int data;
    Node* left;
    Node* right;
    
    Node(int val) : data(val), left(nullptr), right(nullptr) {}
};

void BFS(Node* root) {
    if (!root) return;

    queue<Node*> q;
    q.push(root);
    
    while (!q.empty()) {
        Node* current = q.front();
        q.pop();
        
        cout << current->data << " ";
        
        if (current->left) q.push(current->left);
        if (current->right) q.push(current->right);
    }
}

int main() {
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    
    cout << "BFS Traversal: ";
    BFS(root);
    
    return 0;
}

Output:

BFS Traversal: 1 2 3 4 5

BFS for Graphs

Here is an implementation of BFS for a graph in C++:

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

void BFS(int start, const vector<vector<int>>& graph, vector<bool>& visited) {
    queue<int> q;
    q.push(start);
    visited[start] = true;
    
    while (!q.empty()) {
        int current = q.front();
        q.pop();
        
        cout << current << " ";
        
        for (int neighbor : graph[current]) {
            if (!visited[neighbor]) {
                q.push(neighbor);
                visited[neighbor] = true;
            }
        }
    }
}

int main() {
    int nodes = 6;
    vector<vector<int>> graph(nodes);
    
    // Add edges
    graph[0] = {1, 2};
    graph[1] = {0, 3, 4};
    graph[2] = {0, 4};
    graph[3] = {1, 5};
    graph[4] = {1, 2, 5};
    graph[5] = {3, 4};
    
    vector<bool> visited(nodes, false);
    
    cout << "BFS Traversal starting from node 0: ";
    BFS(0, graph, visited);
    
    return 0;
}

Output:

BFS Traversal starting from node 0: 0 1 2 3 4 5

6. Applications of BFS

Shortest Path in Unweighted Graphs

BFS is often used to find the shortest path between two nodes in an unweighted graph. By exploring nodes level by level, BFS ensures that the first time a target node is reached, it is via the shortest path.

Solving Puzzles (e.g., Maze Problems)

BFS can be applied to grid-based puzzles like mazes, where each cell in the maze is considered a node, and edges represent possible movements between cells. BFS can then explore the maze and find the shortest path to the exit.

tip

There is a cool video on YouTube that demonstrates how BFS can be used to solve a maze.

Web Crawling and Social Networks

In web crawling, BFS explores web pages by visiting each link in a breadth-first manner. This approach ensures that all immediate links are explored before moving deeper. BFS is also used in social networks to discover connections between users, measuring degrees of separation between individuals.

7. Conclusion

In this tutorial, we've covered the basics of BFS, including its concepts, working mechanism, and implementation in C++. We also explored various applications, challenges, and optimizations of BFS. Mastering BFS is crucial for understanding graph traversal algorithms and solving problems in areas like pathfinding, network analysis, and puzzles.

To strengthen your understanding of BFS, try solving these problems:

1. Beginner
   • Find the shortest path in an unweighted graph.
2. Intermediate
   • Solve a maze using BFS.
3. Advanced
   • Implement bidirectional BFS for large graphs.

We have a competitive programming platform, LCOJ, where you can practice these problems and more.

Happy coding!